The difference quotient formula is a part of the definition of the derivative of a function. By taking the limit as the variable h tends to 0 to the difference quotient of a function, we get the derivative of the function. Let us learn the difference quotient formula along with its derivation and examples.
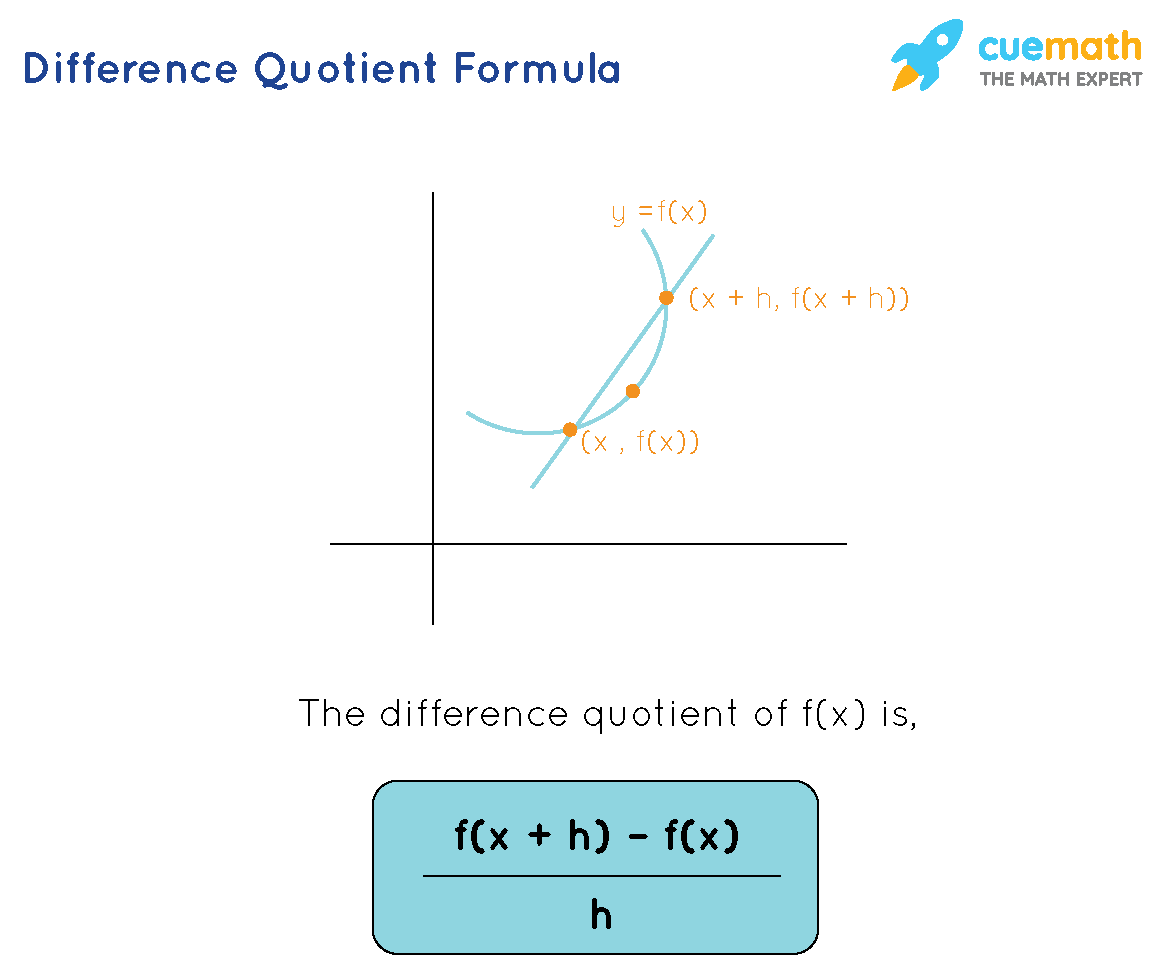
By seeing the name, "difference quotient formula", are you able to recollect something? The words "difference" and "quotient" are giving the feel of the slope formula. Yes, the difference quotient formula gives the slope of a secant line that is drawn to a curve. What is a secant line? A secant line of a curve is a line that passes through any two points of the curve. Let us consider a curve y = f(x) and a secant line that passes through two points of the curve (x, f(x)) and (x + h, f(x + h)). Then the difference quotient of the function f(x) is shown below.

The difference quotient formula of a function y = f(x) is,
Let us consider a function y = f(x) and let a secant line passes through two points of the curve (x, f(x)) and (x + h, f(x + h)). Thus using the slope formula, the slope of the secant line is,
[ f(x + h) - f(x) ] / [ (x + h) - x] = [ f(x + h) - f(x) ] / h [Since the slope of any straight line = change in y/ change in x.)
This is nothing but the difference quotient formula.
Note: As h → 0, the secant of y = f(x) becomes a tangent to the curve y = f(x). Thus, as h → 0, the difference quotient gives the slope of the tangent and hence it gives the derivative of y = f(x). i.e.,
f ' (x) = lim \(_\) [ f(x + h) - f(x) ] / h

Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts
Let us see the applications of the difference quotient formula in the following section.
Example 1: Find the difference quotient of the function f(x) = 3x - 5.
Solution:
Using the difference quotient formula,
= [ (3(x + h) - 5) - (3x - 5) ] / h
= [ 3x + 3h - 5 - 3x + 5 ] / h
Answer: The difference quotient of f(x) is 3.
Example 2 : Find the derivative of f(x) = 2x 2 - 3 by applying the limit as h → 0 to the difference quotient formula.
Solution:
The difference quotient of f(x)
= [ (2(x + h) 2 - 3) - (2x 2 - 3) ] / h
= [ (2 (x 2 + 2xh + h 2 ) - 3) - 2x 2 + 3 ] / h
= [ 2x 2 + 4xh + 2h 2 - 2x 2 + 3 ] / h
By applying the limit as h → 0, we get the derivative f ' (x).
f '(x) = 4x + 2(0) = 4x.
Answer: f ' (x) = 4x.
Example 3: Find the difference quotient of the function f(x) = ln x.
Solution:
Using the difference quotient formula, the difference quotient of f(x) is,
= [ ln (x + h) - ln x ] / h
= ln [ (x + h) / x ] / h (because by quotient property of logarithms, ln m - ln n = ln (m / n))
Answer: The difference quotient of f(x) is, ln [ (x + h) / x ] / h.
The difference quotient formula is nothing but the slope of a secant line formula. The difference quotient of a function y = f(x) is given by [ f(x + h) - f(x) ] / h.
Since the difference quotient is nothing but the slope of a secant line, we use the slope formula to derive the difference quotient formula. The slope of the line joining (x, f(x)) and (x + h, f(x + h)) by slope formula is, [ f(x + h) - f(x) ] / [ (x + h) - x] = [ f(x + h) - f(x) ] / h. This is the difference quotient formula.
The difference quotient formula is mainly used to find the derivative. i.e., the limit of the difference quotient as h → 0 gives the derivative of the function. i.e., f ' (x) = lim \(_\) [ f(x + h) - f(x) ] / h
The limit of the difference quotient of a function f(x) as h → 0 is nothing but the derivative of the function. i.e., the derivative of the function f(x) is, f ' (x) = lim \(_\) [ f(x + h) - f(x) ] / h.